Discrete Math

Bài toán chia kẹo Euler, $n$ biến, tổng $m$

Trường hợp nghiệm không âm

Trường hợp nghiệm dương

Bài toán chọn phần tử

1. Có bao nhiêu cách lấy ra $k$ phần tử trong $n$ phần tử được xếp trên đường thẳng sao cho không có 2 phần tử kề nhau cùng được lấy ra?

   \[S(n,k)=C^k_{n-k+1}\]

2. Có bao nhiêu cách lấy ra $k$ phần tử trong $n$ phần tử được xếp trên đường tròn sao cho không có 2 phần tử kề nhau cùng được lấy ra?

   \[S(n,k)=\frac{n}{n-k}C^k_{n-k}\]

3. Có bao nhiêu dãy gồm $n$ phần tử $a_1,a_2,…,a_n$, trong đó mỗi phần tử lấy giá trị từ ${0,1,2}$ đồng thời không chứa 2 số $0$ đứng liền nhau và cũng không chứa 2 số $1$ đứng liền nhau

   \[S_n=2S_{n-1}+S_{n-2},~S_1=3,~S_2=7\]

4. Có bao nhiêu cách chọn hai tập hợp $A,B \subset C$ khác rỗng sao cho $A \cup B = C$, biết tập $C$ có $n$ phần tử

   \[S(n)=3^{n-1}\]

   Trường hợp $A,B$ có thể rỗng

   \[S(n)=3^n\]

   Trường hợp $A,B$ không rỗng, không giao nhau

   \[S(n)=2^{n-1}-1\]

Bài toán xếp, bài toán đếm

1. Số số nguyên từ $1$ đến $n$ chia hết cho $k$ là

   \[S(n,k)=\left\lfloor\frac{n}{k}\right\rfloor\]

2. Bài toán xếp khách Lucas: Có một bàn tròn, xung quanh có $2n$ ghế. Cần sắp chỗ cho $n$ cặp vợ chồng sao cho các ông ngồi xen kẽ các bà và không có cặp vợ chồng nào ngồi cạnh nhau. Hỏi có bao nhiêu cách xếp?

   \[S(n,k)=2.n!.\left(\sum_{i=0}^n (-1)^i \frac{2n}{2n-i} C^i_n (n-i)!\right)\]

3. Có bao nhiêu số nhị phân $n$ bit mà không có 2 bit $1$ nào cạnh nhau?

   \[S(n)=F_{n+2}, ~F(1)=1, ~F(2)=1\]

4. Có bao nhiêu hoán vị của $(1,2,3,4,…,n)$ sao cho hoán vị $i$ không nằm ở vị trí thứ $i$

   \[S(n)=n!\left( \sum_{k=0}^n \frac{(-1)^k}{k!}\right)= \left\lfloor\frac{n!}{e} +\frac{1}{2}\right\rfloor\]

   Tính chẵn lẻ: $S(1)$ chẵn, $S(2)$ lẻ, ….

5. Có bao nhiêu hoán vị của $(1,2,3,4,…,n)$ sao cho không có 2 số chẵn nào cạnh nhau

   Trường hợp $n = 2k+1$

   \[S(2k+1)=\frac{(k+2)!(k+1)!}{2}\]

   Trường hợp $n=2k$

   \[S(2k)=k!(k+1)!\]

6. Có bao nhiêu hoán vị của $(1,2,3,4,…,n)$ sao cho không có 2 số lẻ nào cạnh nhau

   Trường hợp $n = 2k+1,2k$

   \[S(2k)=S(2k+1)=k!(k+1)!\]

7. Có bao nhiêu số có $k<9$ chữ số mà $a_1<a_2<…<a_k$ hoặc $a_1>a_2>…>a_k$

   \[S(k)=2C^k_9+C^{k-1}_9\]

Bài toán chia miền, phân hoạch

1. Trên mặt phẳng, kẻ $n$ đường thẳng sao cho không có 2 đường thẳng nào song song và 3 đường nào đồng quy. Hỏi mặt phẳng chia làm mấy phần?

   \[S(n)=\frac{n^2+n+2}{2}\]

2. Có bao nhiêu cách phân hoạch tập $n$ phần từ thành $k$ phần khác rỗng

   \[S(n,k)=\frac{1}{k!} \sum_{i=0}^k (-1)^i C^i_k (k-i)^n\]

Bài toán tìm số nhỏ nhất để tồn tại

1. Với $m$ chia hết $k$ bất kỳ, cần chọn ít nhất bao nhiêu số để luôn tồn tại $m$ số có tổng chia hết cho $k$

   \[S(m,k)=m+k-1\]

Hàm sinh

VD: Tìm nghiệm không âm của phương trình $n=a+b+c$ trong đó $0 \le a \le 3,0 \le b \le 2,0 \le c \le 4$

• Đặt $g(x)=(1+x+x^2+x^3)(1+x+x^2)(1+x+x^2+x^3+x^4)$
• Khi đó đáp án là hệ số của $x^n$
• Mở rộng hơn là ta có thể cho chuỗi đa thức vô hạn

Đẳng thức hàm sinh

Xây dựng dãy nhị phân

• Dãy đầu tiên là $0,0,0,0…0$
• Dãy cuối cùng là $1,1,1,..,1$
• Dãy hiện tại $b_1,b_2,…,b_n$

Thuật toán sinh kế tiếp

• Tìm $i$ đầu tiên thỏa mãn $i=0$ (duyệt từ $n$ về $1$)
• Gán lại $b_i=1$ và $b_j=0$ $\forall j >i$ ta được dãy $b_n$ là dãy kế tiếp

Sinh tập con $m$ phần tử của tập $n$ phần tử

• Cho $X={1,2,3,…,n}$
• Tập đầu tiên $1,2,3,…,m$
• Tập cuối cùng là $(n-m+1,n-m+2,…,n)$
• Dãy hiện tại $a_1,a_2,…,a_m$

Thuật toán sinh kế tiếp

• Tìm từ phải sang trái mà phần tử có thể tăng được nữa
• Cộng 1 đơn vị vào phần tử đó, các phần tử tiếp theo là dãy liên tiếp
• Cách tìm ngược
  • Tìm từ phải sang trái phần từ có thể giảm
  • Giảm 1 đơn vị và thay tất cả phía sau thành phần từ cuối ngược lại

Sinh hoán vị tập $n$ phần tử

• Hoán vị đầu tiên $(1,2,3,..,n)$
• Hoán vị cuối cùng $(n,n-1,…,2,1)$
• Hoán vị hiện tại $(a_1,a_2,…,a_n)$

Thuật toán sinh kế tiếp

• Tìm từ bên phải số thỏa mãn $a_j$ thỏa mãn $a_j<a_{j+1}$
• Tìm từ bên phải $a_j$ số nhỏ nhất $a_k$ mà lớn hơn $a_j$
• Đổi chỗ $a_j,a_k$
• Lật ngược $a_{j+1}$ đến $a_n$

Thuật toán quay lui

Cho $A_1,A_2,…,A_n$ là các tập hữu hạn. Ký hiệu $X = A_1 \times A_2 \times … \times A_n = {(x_1,x_2,…,x_n): x_i \in A_i}$

Giả sử $P$ là tính chất cho trên $X$. Tìm tất cả các phần tử của $X$ thỏa mãn tính chất $P$

Các phần tử của $D$ được gọi là lời giải chấp nhận được

Lời giải bộ phận

Ta gọi lời giải bộ phận cấp $k$ là bộ có thứ tự gồm $k$ thành phần $(a_1,a_2,…,a_k)$ trong đó $a_i \in A_i$

Lời giải tổng quát

Giả sử ta đang có lời giải bộ phận cấp $k-1$

Gọi $S_k \subset A_k$ là tập các phần tử có thể chọn cho $a_k$

Mã giả như sau

1
2
3
4
5
6
7
8
def Backtrack(k: integer):
	Xây dựng S_k
		for y in S_k:
			a_k = y
			if k == n:
				Ghi nhận lời giải
			else:
				Backtrack(k+1)

• Đây là trường hợp đẹp nhất, còn trường hợp thông thường là duyệt hết $A_k$ và kiểm tra xem có phù hợp không
• Lệnh để gọi thuật toán quay lui là Backtrack(1)
• Mấu chốt ở đây là chọn $S_k$ sao cho hợp lý

Dưới đây là các tập hợp và $S_k$ của từng bài toán

• Bài toán liệt kê xâu nhị phân

  \[B = \{(x_1,x_2,...,x_n):x_i \in \{0,1\} \}\]

  $S_k = {0,1}$

• Bài toán liệt kê tập con $m$ phần tử của tập $N={1,2,3,…,n}$

  \[S(m,n)=\{(x_1,x_2,...,x_m) \in N^m: 1 \le x_1 < x_2 < .. < x_m \le n\}\]

  $S_k = {a_{k-1}+1,a_{k-1}+2,…,n-m+k}$

• Tập các hoán vị $n$ phần tử $N={1,2,3,…,n}$

  \[S(n)=\{(x_1,x_2,...,x_n) \in N^m:x_i \ne x_j;i \ne j \}\]

  $S_k = N \backslash {a_1,a_2,…,a_{k-1} }$

Đồ thị

1. Đồ thị lẻ cạnh luôn tồn tại một đỉnh bậc chẵn
2. Số đỉnh bậc lẻ luôn luôn là số chẵn

Bài toán đếm số đường đi

1. Đồ thị đầy đủ $K_n$. Số lượng đường đi đơn bắt đầu từ đỉnh $1$ và kết thúc tại đỉnh $n$ là bao nhiêu?

   \[S(n)=(n-2)!\]

Tính liên thông

1. Cho $G$ là đồ thị $n$ đỉnh, $m$ cạnh, $k$ thành phần liên thông, khi đó

   \[m \le \frac{(n-k)(n-k+1)}2\]

   Công thức này có thể kiểm tra tính liên thông bằng cách thay $k=1$. Nếu

   \[|E| > \frac{\left(|V|-1\right)|V|}2~\text{hoặc} |E|<|V|-1\]

   thì đồ thị không liên thông

2. Dấu hiệu kiểm tra tính liên thông
   1. Định lý Dirac: Nếu $G$ là đơn đồ thị vô hướng với $n \ge 3$ đỉnh, và $\forall v, ~deg(v) \ge \frac{n}2$, thì $G$ có chu trình Hamilton → liên thông
   2. Định lý Ore: Nếu $G$ là đơn đồ thị vô hướng với $n \ge 3$ đỉnh, và $deg(u)+deg(v) \ge n$ với mọi cặp đỉnh không kề nhau $u,v$, thì $G$ có chu trình Hamilton → liên thông
3. Đồ thị $k-$liên thông: Nếu như muốn phá vỡ tính liên thông của nó ta phải bỏ ít nhất $k$ đỉnh
4. Mọi đồ thị không có chu trình đều là đồ thị 2 phía

Đồ thị 2 phía

1. Đơn đồ thị được gọi là hai phía khi và chỉ khi không chứa chu trình độ dài lẻ
2. Cho $G$ là đồ thị hai phía $n$ đỉnh và $m$ cạnh, khi đó $m \le \frac{n^2}4$

3. Cho $G$ là đồ thị hai phía $n$ đỉnh và $m$ cạnh. Gọi $K$ và $k$ là bậc lớn nhất và nhỏ nhất của các đỉnh của $G$. Khi đó

   \[k \le \frac{2m}{n} \le K\]

Đồ thị phẳng

1. Đồ thị là phẳng khi và chỉ khi nó không chứa đồ thị con đồng phôi $K_{3,3}$ hoặc $K_5$
2. Đồ thị $Q_n$ không phẳng

Xem đồ thị phẳng liên thông ở phần Công thức Euler

Đồ thị Euler

Đi qua mỗi cạnh đúng 1 lần

1. Đa đồ thị vô hướng liên thông có chu trình Euler khi và chỉ khi nó không có đỉnh bậc lẻ
2. Đa đồ thị vô hướng liên thông có đường đi Euler khi và chỉ khi nó có không quá 2 đỉnh bậc lẻ

Đồ thị Hamilton

Đi qua mỗi đỉnh đúng 1 lần

1. $Q_n~(n \ge 3)$ là đồ thị Hamilton
2. Đồ thị có hai đỉnh bậc 1 → Không là đồ thị Hamilton
3. Đồ thị có 3 đỉnh bậc 1 → Không phải là nửa Hamilton
4. Định lý Dirac: Nếu $G$ là đơn đồ thị vô hướng với $n \ge 3$ đỉnh, và $\forall v, ~deg(v) \ge \frac{n}2$, thì $G$ có chu trình Hamilton
5. Định lý Ore: Nếu $G$ là đơn đồ thị vô hướng với $n \ge 3$ đỉnh, và $deg(u)+deg(v) \ge n$ với mọi cặp đỉnh không kề nhau $u,v$, thì $G$ có chu trình Hamilton.

Cây và rừng

Cây

1. Tính chất cơ bản của cây: Giả sử $T$ là đồ thị $n$ đỉnh. Các mệnh đề sau là tương đương
   1. $T$ là cây
   2. $T$ không chứa chu trình và có $n-1$ cạnh
   3. $T$ liên thông và có $n-1$ cạnh
   4. $T$ liên thông và mỗi cạnh của nó đều là cầu
   5. Hai đỉnh bất kỳ của $T$ nối với nhau bởi đúng 1 đường đi đơn
   6. $T$ không chứa chu trình nhưng cứ thêm 1 cạnh là ta thu được 1 chu trình
2. Mọi cây đều là đồ thị hai phía

Rừng

1. Công thức liên hệ giữa đỉnh cây cạnh của một rừng

   \[\text{Đỉnh}=\text{Cây}+\text{Cạnh}\]

Bài toán đếm số cây khung

Ma trận Laplace

Cho đồ thị có các đỉnh $v_1,v_2,…,v_n$. Ma trận Laplace $L$ là ma trận $V \times V$ thỏa mãn

• Đếm số cây khung bằng cách tính định thức ma trận của phần bù đại số bất kỳ của $L$
  • Nói đơn giản, bỏ cột đầu và hàng đầu và tính định thức của nó là ra số cây khung
• Số giá trị đặc trưng nhận giá trị $0$ là số thành phần liên thông

Đếm số cây khung của đồ thị 2 phía đầy đủ $K_{m,n}$

Đếm số cây khung của đồ thị ô lưới

$G_k(n)$ là đồ thị ma trận $k \times n$ ô lưới

Dưới đây là công thức truy hồi của một số cây khung đồ thị

• $k=2$

  \[T(n)=4T(n-1)-T(n-2)\] \[T=\{1, 4, 15, 56, 209, . . .\}\]

• $k=3$

  \[T(n) = 15T(n−1) − 32T(n−2) + 15T(n−3) − T(n−4)\] \[T=\{1, 15, 192, 2415, 30305, . . .\}\]

Công thức Euler

Cho $G$ là đồ thị liên thông phẳng, $D$ là số đỉnh, $M$ là số mặt, $C$ là số cạnh thì ta có biểu thức liên hệ

Hệ quả với đồ thị phẳng liên thông

• $G$ là đồ thị phẳng liên thông với $n \ge 3$ đỉnh, $m$ cạnh thì ta có

  \[m \le 3n-6\]

• $G$ là đồ thị phẳng liên thông $n$ đỉnh và $m$ cạnh không chứa tam giác

  \[m \le 2n-4\]

Tô màu đồ thị

Tô màu đồ thị là tô mỗi đỉnh 1 màu sao cho hai đỉnh kề nhau thì không chung màu

Định lý 4 màu: Mọi bản đồ hành chính đều có thể tô bởi bốn màu sao cho không có 2 đơn vị hành chính có chung biên giới nào bị tô bởi cùng màu.

Đồ thị đối ngẫu

Đồ thị đối ngẫu $G^*$ của đồ thị $G(V,E)$ với các tập miền $R$ là đồ thị với tập đỉnh và cạnh

• Tập đỉnh của $G^*$ là miền $R$
• Hai miền có cạnh chung thì được nối với nhau

Sắc số

$\chi(G)$ là số $c$ nhỏ nhất sao cho có thể tô được đỉnh của $G$ bởi $c$ màu

• $\chi(G)=2$ nếu $G$ là đồ thị hai phía và ngược lại
• $\chi(G) \ge \triangle G$ (là số bậc lớn nhất)
• Mọi đồ thị phẳng đều tô được bởi 4 màu
• $\chi(G) \le \triangle (G)+1$ với $G$ là đơn đồ thị vô hướng

Thuật toán tham lam

• Khởi tạo: Sắp xếp các đỉnh theo thứ tự $v_1,v_2,…,v_n$, tô $v_1$ màu $1$
• Với $2 \le j \le n$:
  • Tô màu $k >0$ là chỉ số nhỏ nhất cho đỉnh $v_j$ khác màu với đỉnh kề nó

Tô màu cạnh

Tô màu cạnh của đồ thị sao cho không có 2 cạnh nào chung đỉnh tô bởi 1 màu

Số màu ít nhất sử dụng để tô màu cạnh của đồ thị $G$ được gọi là sắc số cạnh và ký hiệu là $\chi’(G)$

Đối với đơn đồ thị hai phía $G$ thì ta có

Biểu diễn đồ thị

• Giả sử các đỉnh được đánh số theo thứ tự từ $1$ đến $|V|=n$
• Có $|E|=m$

Ma trận kề

Ma trận $A$ kích thức $n \times n$ xác định với $a_{ij}=1$ nếu đỉnh $i,j$ nối với nhau

Tức là nhìn từ số từ cột sang hàng

Tính chất ma trận kề của đồ thị vô hướng

• $A=A^T$

Ma trận trọng số

Khác với ma trận kề thì $a_{ij} = k$ với $k >0$ thì nếu đỉnh $i,j$ nối với nhau và có trọng số $k$

Các thuật toán duyệt đồ thị

Duyệt theo chiều rộng của đồ thị vô hướng (BFS)

Độ phức tạp $O(|V|+|E|)$

• Chọn đỉnh bắt đầu
• Duyệt tất cả các con của nó theo thứ tự từ điển
• Vào các con của nó duyệt các con của nó tiếp,

Ứng dụng:

• Tìm đường đi ngắn nhất theo số cạnh
• Kiểm tra tính liên thông

Duyệt theo chiều sâu của đồ thị (DFS)

Độ phức tạp $O(|V|+|E|)$

• Chọn đỉnh bắt đầu
• Duyệt con đầu tiên của nó theo thứ tự từ điển
  • Bình thương là màu đen
  • Nếu duyệt lại phần tử trong cây
    • Cạnh ngược (từ con tới tổ tiên) → Quy ước màu đỏ
    • Cạnh tới (từ tổ tiên tới cháu) → Quy ước màu xanh dương
    • Cạnh vòng (không có quan hệ họ hàng) → Quy ước màu xanh lá
• Nếu không còn con thì leo lên cha duyệt con thứ
  • Điểm mà bị leo thì được thêm vào danh sách Topo $T$

Ứng dụng:

• Tìm đường đi từ $s \rightarrow{} t$
• Kiểm tra liên thông
• Phát hiện chu trình:
  • Đồ thị không chứa chu trình khi và chỉ khi DFS không phát hiện ra cạnh ngược
• Kiểm tra liên thông mạnh
• Định hướng đồ thị

Thứ tự Topo

Đồ thị không có chu trình $\leftrightarrow{}$ DFS không có cạnh ngược $\leftrightarrow{}$ Sắp được Topo

• Thứ tự Topo là một thứ tự sắp xếp của các đỉnh trong một đồ thị có hướng sao cho mỗi cạnh trong đồ thị chỉ đi từ một đỉnh có thứ tự nhỏ hơn đến một đỉnh có thứ tự lớn hơn

Kiểm tra Topo

• Nếu có 1 đỉnh $u$ trước $v$ mà nó không có cạnh trong đồ thị
• DFS đồ thị trên
• Thứ tự Topo duyệt theo cây từ trên xuống dưới

Thứ tự Topo là đảo ngược của danh sách Topo $T$

Bài toán cây khung nhỏ nhất

Cây khung của đồ thị

Giả sử $G=(V,E)$ là đồ thị vô hướng liên thông. Cây $T=(V,F)$ với $F \subset E$ được gọi là cây khung của $G$

Định lý: Số cây khung của đồ thị $K_n$ là $n^{n-2}$

Bài toán đường đi ngắn nhất

Thuật toán Dijiktra

Bất đẳng thức cận trên: Gọi $d[v]$ là cận trên độ dài đường đi ngắn nhất từ đỉnh $1 \rightarrow{} v$, với mỗi đỉnh $u,v$ sao cho có cạnh từ $u \rightarrow{} v$, ta luôn có

Thứ tự các đỉnh được tìm thấy trong quá trình tìm kiếm đường đi ngắn nhất sẽ sắp xếp theo khoảng cách đối với đồ thị có trọng số không âm (mình nghĩ vậy)

• Các mệnh đề cần lưu ý
  • Nếu nhân đôi trọng số, thuật toán không đổi thứ tự các đỉnh
  • Nếu thay đổi trọng số mà vẫn giữ bất đẳng thức thì thuật toán cũng k đổi
  • Nếu thay đổi trọng số mà vẫn không giữ bất đẳng thức thì thuật toán sẽ đổi

Bài toán luồng cực đại

Mạng

Mạng là đồ thị có hướng $G=(V,E)$

• Có duy nhất một đỉnh $s$ không có cung đi vào gọi là đỉnh phát (nguồn) và duy nhất một đỉnh $t$ không có cung đi ra gọi là đỉnh thu (đích)

• Mỗi cung $e$ của $G$ được gắn với số không âm $c(e)$ được gọi là khả năng thông qua của $e$

  

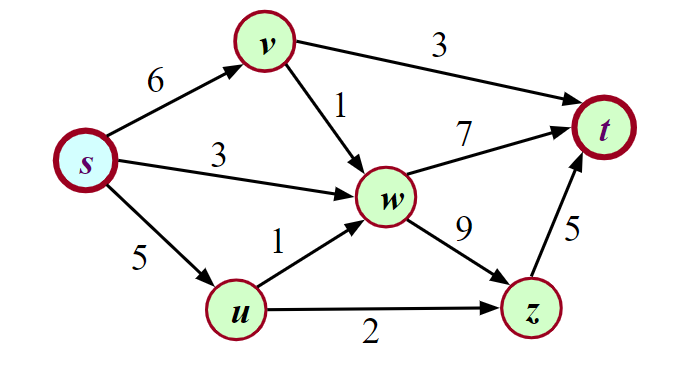
Luồng trong mạng

Luồng $f$ trong mạng $G=(V,E)$ là phép gán số $f(e)$ cho mỗi cạnh $e$ thỏa mãn điều kiện

1. $0 \le f(e) \le c(e)$

2. Với mỗi $v \ne s,t$

   \[\sum_{e \in E(v^-)} f(e)=\sum_{e \in E(v^+)} f(e)\]

   Tức luồng ra = luồng vào tại mỗi đỉnh

3. Giá trị của luồng $f$

   \[val(f)=\sum_{e \in E(s^+)} f(e)=\sum_{e \in E(t^-)} f(e)\]

Ước lượng luồng cực đại

• Xét 1 điểm thay trọng số
  • Thay tất cả cạnh đi vào
    • Thay cạnh đi vào bằng min(tổng max đi ra, cạnh đi vào)
  • Thay tất cả cạnh đi ra
    • Thay cạnh đi ra bằng min(tổng max đi vào, cạnh đi ra)
• Lược bỏ mạng con
  • Một mạng con là 1 mạng có 1 đỉnh là phát giả $s$ và 1 đỉnh là thu giả $t$ trong đó
    • Đỉnh thu giả $t$ không có đường đi tới các đỉnh nào trong mạng
    • Không có đỉnh nào trong mạng có đường đi tới đỉnh phát giả $s$
    • Không có đỉnh nào trong mạng con (trừ $s,t$) có đường đi tới các đỉnh ngoài mạng con → Có thể thay mạng con thành 1 đường đi duy nhất là $s$ → $t$ sao cho đường đó có trọng số = min(tổng ra s, tổng vào t)

Tìm cực đại bằng cách dùng lát cắt

• Lát cắt là cách phân hoạch tập đỉnh $(S,T)$ sao cho $s \in S, t\in T$

• Lát cắt cực tiểu là lát cắt sao cho $cap = max~val$

• Previous
  My Lope
• Next
  Giải tích 3